roc_curve() constructs the full ROC curve and returns a
tibble. See roc_auc() for the area under the ROC curve.
Usage
roc_curve(data, ...)
# S3 method for class 'data.frame'
roc_curve(
data,
truth,
...,
na_rm = TRUE,
event_level = yardstick_event_level(),
case_weights = NULL,
options = list()
)Arguments
- data
A
data.framecontaining the columns specified bytruthand....- ...
A set of unquoted column names or one or more
dplyrselector functions to choose which variables contain the class probabilities. Iftruthis binary, only 1 column should be selected, and it should correspond to the value ofevent_level. Otherwise, there should be as many columns as factor levels oftruthand the ordering of the columns should be the same as the factor levels oftruth.- truth
The column identifier for the true class results (that is a
factor). This should be an unquoted column name although this argument is passed by expression and supports quasiquotation (you can unquote column names). For_vec()functions, afactorvector.- na_rm
A
logicalvalue indicating whetherNAvalues should be stripped before the computation proceeds.- event_level
A single string. Either
"first"or"second"to specify which level oftruthto consider as the "event". This argument is only applicable whenestimator = "binary". The default uses an internal helper that defaults to"first".- case_weights
The optional column identifier for case weights. This should be an unquoted column name that evaluates to a numeric column in
data. For_vec()functions, a numeric vector,hardhat::importance_weights(), orhardhat::frequency_weights().- options
[deprecated]No longer supported as of yardstick 1.0.0. If you pass something here it will be ignored with a warning.
Previously, these were options passed on to
pROC::roc(). If you need support for this, use the pROC package directly.
Value
A tibble with class roc_df or roc_grouped_df having
columns .threshold, specificity, and sensitivity.
Details
roc_curve() computes the sensitivity at every unique
value of the probability column (in addition to infinity and
minus infinity).
There is a ggplot2::autoplot() method for quickly visualizing the curve.
This works for binary and multiclass output, and also works with grouped
data (i.e. from resamples). See the examples.
Multiclass
If a multiclass truth column is provided, a one-vs-all
approach will be taken to calculate multiple curves, one per level.
In this case, there will be an additional column, .level,
identifying the "one" column in the one-vs-all calculation.
Relevant Level
There is no common convention on which factor level should
automatically be considered the "event" or "positive" result
when computing binary classification metrics. In yardstick, the default
is to use the first level. To alter this, change the argument
event_level to "second" to consider the last level of the factor the
level of interest. For multiclass extensions involving one-vs-all
comparisons (such as macro averaging), this option is ignored and
the "one" level is always the relevant result.
See also
Compute the area under the ROC curve with roc_auc().
Other curve metrics:
gain_curve(),
lift_curve(),
pr_curve()
Examples
# ---------------------------------------------------------------------------
# Two class example
# `truth` is a 2 level factor. The first level is `"Class1"`, which is the
# "event of interest" by default in yardstick. See the Relevant Level
# section above.
data(two_class_example)
# Binary metrics using class probabilities take a factor `truth` column,
# and a single class probability column containing the probabilities of
# the event of interest. Here, since `"Class1"` is the first level of
# `"truth"`, it is the event of interest and we pass in probabilities for it.
roc_curve(two_class_example, truth, Class1)
#> # A tibble: 502 × 3
#> .threshold specificity sensitivity
#> <dbl> <dbl> <dbl>
#> 1 -Inf 0 1
#> 2 1.79e-7 0 1
#> 3 4.50e-6 0.00413 1
#> 4 5.81e-6 0.00826 1
#> 5 5.92e-6 0.0124 1
#> 6 1.22e-5 0.0165 1
#> 7 1.40e-5 0.0207 1
#> 8 1.43e-5 0.0248 1
#> 9 2.38e-5 0.0289 1
#> 10 3.30e-5 0.0331 1
#> # ℹ 492 more rows
# ---------------------------------------------------------------------------
# `autoplot()`
# Visualize the curve using ggplot2 manually
library(ggplot2)
library(dplyr)
roc_curve(two_class_example, truth, Class1) %>%
ggplot(aes(x = 1 - specificity, y = sensitivity)) +
geom_path() +
geom_abline(lty = 3) +
coord_equal() +
theme_bw()
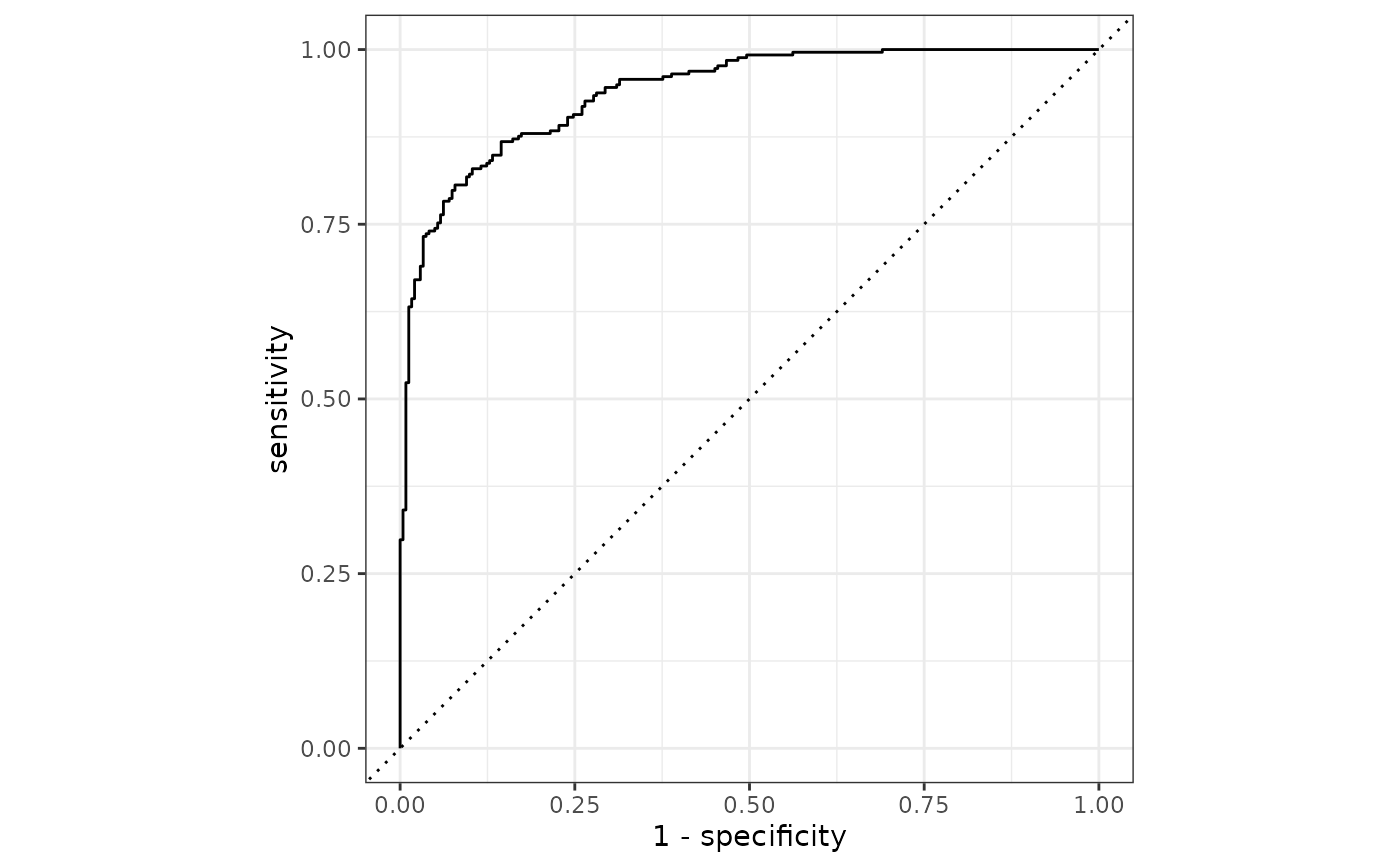 # Or use autoplot
autoplot(roc_curve(two_class_example, truth, Class1))
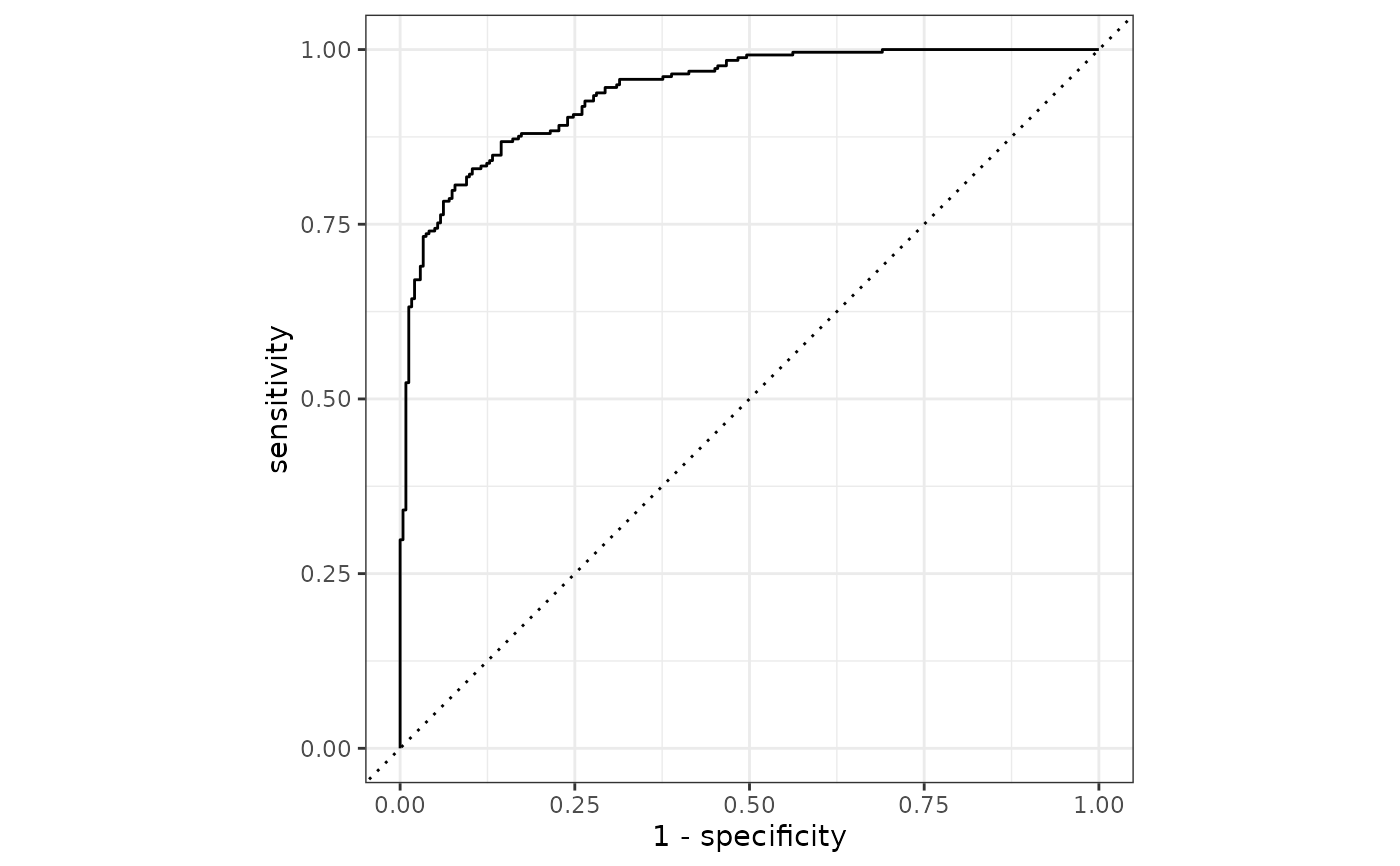
# Or use autoplot
autoplot(roc_curve(two_class_example, truth, Class1))
 if (FALSE) { # \dontrun{
# Multiclass one-vs-all approach
# One curve per level
hpc_cv %>%
filter(Resample == "Fold01") %>%
roc_curve(obs, VF:L) %>%
autoplot()
# Same as above, but will all of the resamples
hpc_cv %>%
group_by(Resample) %>%
roc_curve(obs, VF:L) %>%
autoplot()
} # }
if (FALSE) { # \dontrun{
# Multiclass one-vs-all approach
# One curve per level
hpc_cv %>%
filter(Resample == "Fold01") %>%
roc_curve(obs, VF:L) %>%
autoplot()
# Same as above, but will all of the resamples
hpc_cv %>%
group_by(Resample) %>%
roc_curve(obs, VF:L) %>%
autoplot()
} # }
